Les exercices python à connaître

On souhaite construire des arbres binaires parfaits « additifs ». Dans ces arbres :

• tous les niveaux sont entièrement remplis ;
• la valeur d'un nœud intérieur est toujours égale à la somme des valeurs de ses enfants.

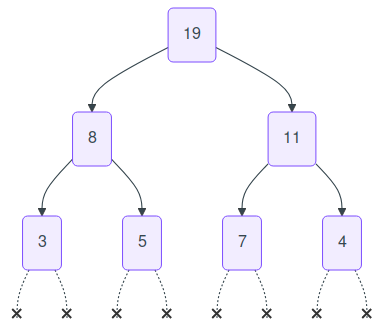
Un exemple d'arbre binaire additif: Cet arbre est :

• parfait (tous ses niveaux sont remplis) ;

• additif (on a 3 + 5 = 8 ; 7 + 4 = 11 ; 8 + 11 = 19).

Représentation des arbres en machine:
On représente les arbres binaires ainsi :

• l'arbre vide est représenté par None,
• un arbre non vide est représenté par un tuple (sous-arbre gauche, valeur, sous-arbre droit).

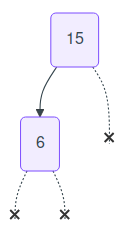
Ainsi le tuple ((None, 6, None), 15, None) représente l'arbre suivant :

On demande de compléter la fonction arbre_additif qui prend en argument la liste valeurs contenant les valeurs des feuilles et renvoie l'arbre correspondant représenté à l'aide de tuples.
On garantit que le nombre d'éléments de valeurs est une puissance de 2 strictement positive. Ces éléments sont tous des nombres entiers.
Exemples :
>>> arbre_additif([6])
(None, 6, None)
>>> arbre_additif([6, 9])
((None, 6, None), 15, (None, 9, None))
>>> arbre_additif([3, 5, 7, 4])
(((None, 3, None), 8, (None, 5, None)), 19, ((None, 7, None), 11, (None, 4, None)))

On commence en construisant une liste contenant les feuilles. On calcule ensuite la liste contenant les nœuds du niveau supérieur.
Ce calcul effectué, on remplace la liste des nœuds par la nouvelle et on répète la démarche jusqu'à atteindre la racine.

source : https://codex.forge.apps.education.fr