Les exercices python à connaître

Armé de sa pioche, Steve est à la surface d'une mine. Une étude précise du terrain lui a permis de mesurer la richesse de chaque "bloc" de la mine.

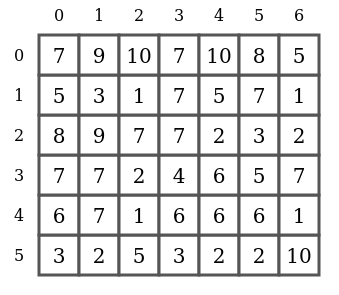
Comme on peut le voir, toutes les richesses sont des nombres entiers positifs.
Ces richesses sont fournies dans une liste de listes Python :
mine = [[7, 9, 10, 7, 10, 8, 5],
      [5, 3, 1, 7, 5, 7, 1],
      [8, 9, 7, 7, 2, 3, 2],
      [7, 7, 2, 4, 6, 5, 7],
      [6, 7, 1, 6, 6, 6, 1],
      [3, 2, 5, 3, 2, 2, 10]]

Ainsi, le 9 sur la troisième ligne, deuxième colonne, indique que le bloc de coordonnées (i, j) = (2, 1) a une richesse de mine[2][1] = 9. De façon générale, dans la notation mine[i][j], i désigne l'indice de la ligne et j celui de la colonne.
On garantit que la mine possède au moins une ligne et deux colonnes.
Afin de ne pas user prématurément sa pioche, Steve ne souhaite pas creuser l'intégralité de la mine. À chaque niveau, il envisage plutôt de creuser soit :

• vers le bas à gauche,
• vers le bas,
• vers le bas à droite.

Lorsque Steve creuse un bloc, il récupère la richesse de celui-ci. Ainsi, en partant du bloc de gauche de la première ligne et en creusant toujours sous ses pieds, il gagnerait un total de 7 + 5 + 8 + 7 + 6 + 3 = 36.

Lorsqu'il atteint le fond de la mine (la dernière ligne de la grille), Steve trouve sous ses pieds une roche sombre incassable : il ne peut plus creuser !

Il se demande donc quel est le meilleur filon à explorer : quelles richesses cumulées maximales peut-il espérer accumuler en creusant à partir de chacun des points de la surface et surtout, parmi celles-ci, laquelle est la meilleure ?

La figure suivante met en évidence un des chemins de richesse cumulée maximale. Elle vaut 10 + 7 + 7 + 6+ 10 = 46.

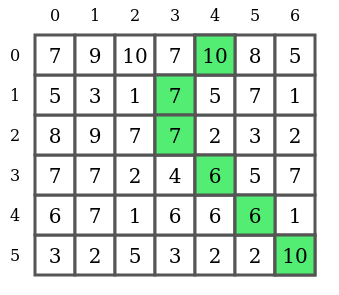
Son raisonnement est le suivant : " Si je suis en un bloc précis, la richesse cumulée maximale que je peux obtenir à partir de ce bloc est égale à la somme :

• de la richesse de ce bloc,
• et de la richesse maximale d'un des trois blocs inférieurs que je peux explorer. "

Afin de résoudre ce problème, on fournit une fonction dimensions renvoyant un tuple formé de la hauteur et de la largeur de la "mine" :
On pourra utiliser cette fonction en faisant : hauteur, largeur = dimensions(mine).

Écrire la fonction meilleure_richesse_cumulee :

• prenant en arguments la mine (liste de listes),
• et renvoyant la plus grande richesse cumulée que l'on peut obtenir à partir d'un des blocs de la surface.

Exemples :
>>> mine = [[1, 2, 3],
      [0, 1, 0],
      [0, 1, 0],
      [4, 0, 0]]
>>> meilleure_richesse_cumulee(mine)
9


>>> mine = [[1, 2, 5]]
>>> meilleure_richesse_cumulee(mine)
5

Exemples :
>>> mine = [[7, 9, 10, 7, 10, 8, 5],
      [5, 3, 1, 7, 5, 7, 1],
      [8, 9, 7, 7, 2, 3, 2],
      [7, 7, 2, 4, 6, 5, 7],
      [6, 7, 1, 6, 6, 6, 1],
      [3, 2, 5, 3, 2, 2, 10]]
>>> meilleure_richesse_cumulee(mine)
46

La fonction calculera de façon itérative les richesses cumulées de chaque niveau i en commençant par le bas de la mine et en remontant vers la surface. Ces valeurs seront stockées dans la liste richesses_cumulees.

A chaque étape, on calculera les richesses d'un niveau à l'aide des valeurs de richesses cumulées du niveau du dessous. Ces calculs se feront dans une liste temporaire temp. On parcourra alors les colonnes j en prenant soin de traiter séparément les colonnes de gauche et de droite de la mine (certains des voisins du niveau inférieur sont alors absents).

Une fois les calculs de la nouvelle ligne terminés, on remplacera la valeur de richesses_cumulees par celle de temp avant d'aborder une nouvelle ligne.

La fonction calculera donc les richesses cumulées depuis le fond de la mine et en remontant ligne par ligne vers la surface.

En dernier lieu, elle renverra la valeur maximale des richesses cumulées du niveau 0.

source : https://codex.forge.apps.education.fr