Les exercices python à connaître

Dans une grille de taille \(n×m\), on souhaite compter tous les chemins allant du coin inférieur gauche (au Sud-Ouest) vers le coin supérieur droit (au Nord-Est).
Les seuls mouvements autorisés sont :

• ↑ Aller au Nord d'une unité.
• → Aller à l'Est d'une unité.
• ↗ Aller au Nord-Est en diagonale, sur le prochain nœud.

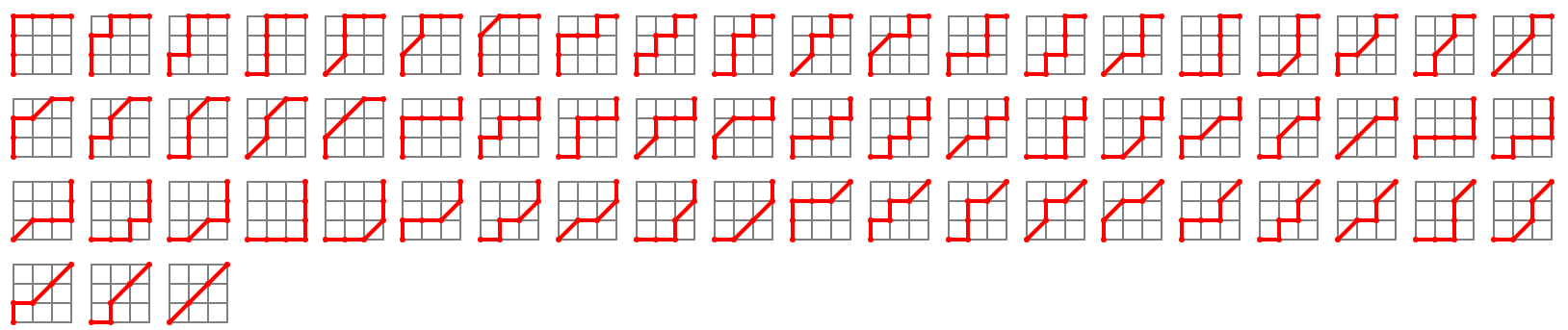
Les chemins pour aller de (0, 0) à ((3, 3) :

Pour écrire une fonction delannoy qui prend en paramètres deux entiers n et m et renvoie le nombre de chemins allant de (0, 0) jusqu'à (n, m), on remarquera :

• Si n ou m est nul,
  • alors le seul chemin est en ligne droite, la réponse est 1,
• sinon, n et m sont non nuls et les chemins qui vont en (n, m) se répartissent en trois catégories :
  • ceux qui venaient de (n - 1, m ),
  • ceux qui venaient de (n , m - 1),
  • ceux qui venaient de (n - 1, m - 1).
  Cces trois catégories sont distinctes et se comptent bien par récursivité.

On utilisera un dictionnaire pour mémoriser les résultats intermédiaires.

Exemples :
>>> delannoy(3, 3)
63
>>> delannoy(2, 31)
5

source : https://codex.forge.apps.education.fr